In this tutorial you learn how to

  • set up custom problems
  • define solutions to them
  • work with trivial solutions
  • plot problems and solutions
  • compute the displacements and von Mises stresses for solutions and how to plot them

The Problem class

Custom problem objects

In this first lesson we explain how to use our DL4TO framework to generate custom TO problems. This is done via the Problem class, which contains all information of the underlying TO problem one intends to solve. We focus on isotropic materials that are linearly elastic. This comprises most common materials, e.g., including steel and aluminum. Since we perform optimization on structured grids, all information is either in scalar or in tensor form. This makes data compatible with DL applications since it allows for a shape-consistent tensor representation.

Let $(n_x, n_y, n_z)$ be the number of voxels in each spacial direction, i.e. the shape of the TO problem. We can create unique problem objects characterized by the following inputs:

  • Scalar material properties that define the physical proporties of the underlying material. These include:

    • Young's modulus $E>0$
    • Poisson's ratio $\nu\in [0, 0.5]$
    • The yield stress $\sigma_{ys}>0$

  • A three-dimensional vector $h$ that defines the voxel sizes in meters in each direction.

  • A binary ($3\times n_x \times n_y \times n_z$)-tensor called $\Omega_\text{dirichlet}$ which we use to encode the presence of directional homogeneous Dirichlet boundary conditions for every voxel. These boundary conditions determine where the structure is "locked" in place, i.e. where the displacements are fixed at 0. $1$s indicate the presence, and $0$s the absence of homogeneous Dirichlet boundary conditions. Currently, we do not support non-homogeneous Dirichlet boundary conditions (i.e. voxels that have displacements fixed at some value $\neq 0$) since we believe that they are not required for most TO tasks.

  • A ($1\times n_x \times n_y \times n_z$)-tensor called $\Omega_\text{design}$ containing values $\in \left\lbrace 0,1,-1\right\rbrace$ that we use to encode design space information. We use $0$s and $1$s to constrain voxel densities to be $0$ or $1$, respectively. Entries of $-1$ indicate a lack of density constraints, which signifies that the density in that voxel can be freely optimized.

  • A ($3\times n_x \times n_y \times n_z$)-tensor called $F$, which encodes external forces given in $\text{N}/\text{m}^3$. The three channels correspond to the force magnitudes in each spacial dimension. For voxels that have external loads assigned to them we automatically enforce the corresponding density value to be $1$.

We can manually create a problem object by defining all the required tensors by hand. For example:

import torch

# scalar material properties
E = 7e10 # Young's modulus (in Pascal)
ν = .3 # Poisson's ratio
σ_ys = 4.5e8 # Yield stress (in Pascal)

shape = [40, 4, 8] # number of voxels in x, y and z direction
h = [0.0250, 0.0250, 0.0250] # spacial dimensions of each voxel in x, y and direction (in meters)

# define external forces
F = torch.zeros(3, *shape)
F[-1, :, :, -1] = -4e7 # external forces (in Newton)

# define locations of homogeneous Dirichlet conditions
Ω_dirichlet = torch.zeros(3, *shape)
Ω_dirichlet[:, 0, :, :] = 1

# define design space
Ω_design = -torch.ones(1, *shape) # -1s indicate that these voxels can be freely optimized
Ω_design[:,:2,:,:] = 1. # we set densities to 1 where there are Dirichlet boundary conditions
Ω_design[:,:,:,-2:] = 1. # we set densities to 1 where there are external forces

We can then generate a custom problem object:

from dl4to.problem import Problem

problem = Problem(E, ν, σ_ys, h, Ω_dirichlet, Ω_design, F, restrict_density_for_voxels_with_applied_forces=False)

The shape of the problem can be accessed via:

problem.shape

torch.Size([40, 4, 8])

In the following, will refer to this specific TO problem as the "ledge" problem.

Three-dimensional interactive plotting

The problem class comes with several useful functionalities. One of them is interactive 3d plotting. We can use it to plot a visualization of our ledge problem:

#output: false
camera_position = (0, 0.35, 0.2)
problem.plot(camera_position=camera_position,
             show_axislabels=True,
             show_ticklabels=True,
             display=False)

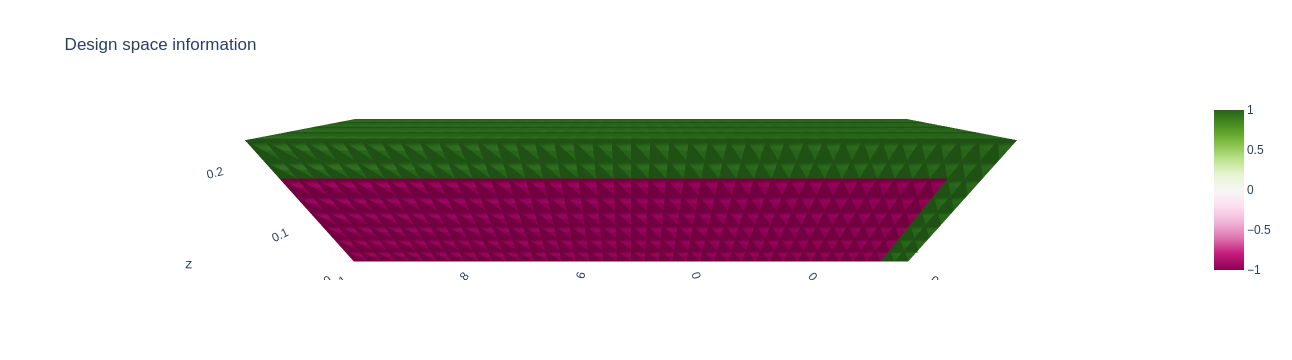
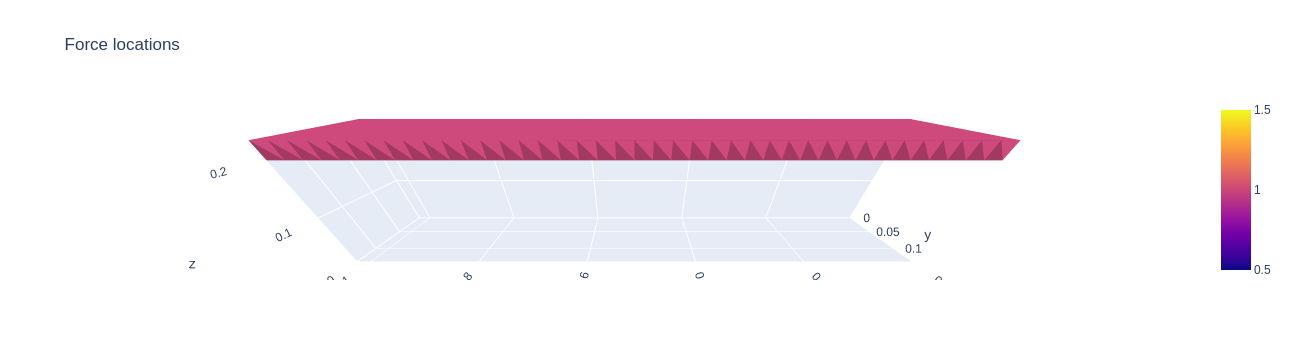
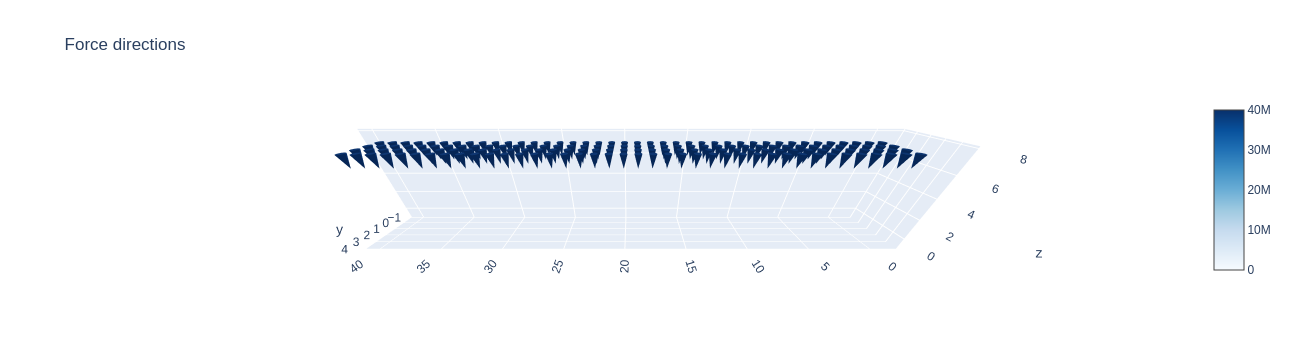
dirichlet design force_loc force_dir

Note: Please change the argument display to display=True if you run the experiments on your machine.

As you can see, we have sucessfully created a TO problem that is locked at the right side and is loaded with external forces pushing downwards from above.

We think that our implementation of TO problems is very flexible but also intuitive to use, especially if you have experience with Numpy or PyTorch. While it is possible to generate custom problems in the way described above, you can also load pre-defined problems from one of the datasets that we provide. We will introduce our datasets and dataloaders a bit later in this tutorial. For now, we continue with an introduction of our Solution class.

The Solution class

Custom solution objects

Objects of this class define solutions to TO problems. They usually result from to application of a TO solver to a problem (we will see that a bit later), but can also be instantiated manually by passing a problem and a density distribution. As an example, we start with a density distribution that contains only zeros:

from dl4to.solution import Solution

θ = torch.zeros(1, *shape)
solution_zeros = Solution(problem, θ)

Here, $\theta$ is a ($1\times n_x \times n_y \times n_z$)-tensor that defines a three-dimensional density distribution for the TO problem. Constructing a solution object like this clearly only works if $\theta$ is known. Usually, this is not the case. Nonetheless, it can sometimes be informative to check specific pre-defined densities, like in this example.

The Solution class provides several useful functionalities, again including interactive 3d plotting:

solution_zeros.plot(camera_position=camera_position,
                   display=False)

zero_density

As we can see, the density distribution $\theta$ has been modified inside of the solution object such that it is not $0$ everywhere anymore. More precisely, it has been adjusted according to the design space information that we prescribed in the problem formulation: We enforced densities of $1$ at certain voxels by setting $\Omega_\text{dirichlet}$ to $1$.

We can check that the density distribution inside of the solution object has indeed been modified and this is not just the visualization:

assert torch.any(solution_zeros.θ != 0)
assert torch.all(θ == 0)

Trivial solutions

The easiest type of solution is what we call a "trivial solution". The density distribution of a trivial solution in $1$ everywhere, where it is permitted (i.e. where $\Omega_\text{design}$ is not $0$). Together with the zero-density example above this therefore constitutes the simplest solution to a TO problem - we simply choose the thickest possible structure!

Each problem object directly comes with its own trivial solution. It can be accessed via:

trivial_solution = problem.trivial_solution

The trivial solution is just simply a solution object from the solution class. Therefore, we can also use our plotting functionality on it:

trivial_solution.plot(camera_position=camera_position,
                      display=False)

trivial_density

Since we do not restrict the density to be $0$ anywhere, the trivial solution is simply a full, solid block. It is interesting to check if this trivial solution actually holds the applied loads and does not break. If this structure would break, applying any TO algorithm would certainly not lead to promising results - because this is already the most solid structure possible.

Solving the PDE for linear elasticity

In order to evaluate the stresses we need to solve the partial differential equation (PDE) of linear elasticity. This library comes with its own in-built finite differences method (FDM) solver, which solves the PDE for us. We found handling with finite differences easier than with finite elements. This is attributed to the regular grid structure, which makes the FDM a suitable and intuitive approach. It is however also possible to include custom PDE solvers, e.g., learned PDE solvers - which we will discuss later.

PDE solvers are passed to problem instances:

from dl4to.pde import FDM

problem.pde_solver = FDM()

Passing PDE solvers to problems (instead of passing them to solutions or TO solvers) my seem unintuitive at first, but it comes with several advantages: First, all solution objects that are derived from this problem will also have access to the PDE solver. The same holds for all TO solver algorithms that we apply to this problem. Second, our implementation automatically constructs most of the PDE system matrix in the background when it is passed to a problem. This saves a lot of time for all future evaluations.

We can now use this FDM solver to solve the PDE. This is done via the "solve_pde" command, which returns three tensors:

  • The displacements $u$, which is a ($3\times n_x \times n_y \times n_z$)-tensor.
  • The stresses $\sigma$, which is a symmetric ($9\times n_x \times n_y \times n_z$)-tensor.
  • The von Mises stresses $\sigma_\text{vM}$, which is a ($1\times n_x \times n_y \times n_z$)-tensor, i.e., a scalar field.
u, σ, σ_vm = trivial_solution.solve_pde()

After the PDE has been solved for a solution, the displacements $u$ are stored inside the solution object and can be accessed via "trivial_solution.u". This avoids solving the same PDE several times.

In order to check if the von Mises stresses are too large, we need to compare its maximum to the yield stress $\sigma_\text{ys}$ of the material:

σ_vm.max() / problem.σ_ys

tensor(0.1249)

Since the fraction returns a value below $1$, this indicates that the structure indees holds the applied forces and does not break!

We can also visualize the spacial distribution of the (normed) displacements and von Mises stresses by passing "solve_pde=True" to the plotting function:

trivial_solution.plot(camera_position=camera_position,
                      solve_pde=True,
                      display=False)

trivial_density_theta trivial_density_u trivial_density_stress

It is interesting to compare this to the PDE solution that we get from our zero-solution that we defined earlier:

u, σ, σ_vm = solution_zeros.solve_pde()
σ_vm.max() / problem.σ_ys

tensor(1.1998)

Since the value is above $1$, this minimial structure does not hold.

In the three-dimensional visualization we can see that this is especially due to very high von Mises stresses in the top right corner:

solution_zeros.plot(camera_position=camera_position,
                    solve_pde=True,
                    display=False)

zero_density_theta zero_density_u zero_density_stress

There is also the option to use pyvista for plotting (instead of the default plotly interface). In the next tutorial, we will show how we can use pyvista for smoother visualizations.

You can save and load problem and solution objects via torch.save(problem, "problem.pt") and problem = torch.load("problem.pt").