The Problem class contains all information of the underlying topology optimization (TO) problem one intends to solve. We focus on isotropic materials that are linearly elastic. This comprises most common materials, e.g., including steel and aluminum. Since we perform optimization on structured grids, all information is either in scalar or in tensor form. This makes data compatible with DL applications since it allows for a shape-consistent tensor representation. Let $(n_x, n_y, n_z)$ be the number of voxels in each spacial direction, i.e. the shape of the TO problem.
We can create unique problem objects characterized by the following inputs:
Scalar material properties that define the physical proporties of the underlying material. These include:
- Young's modulus $E>0$
- Poisson's ratio $\nu\in [0, 0.5]$
- The yield stress $\sigma_{ys}>0$
A three-dimensional vector $h$ that defines the voxel sizes in meters in each direction.
A binary ($3\times n_x \times n_y \times n_z$)-tensor called $\Omega_\text{dirichlet}$ which we use to encode the presence of directional homogeneous Dirichlet boundary conditions for every voxel. These boundary conditions determine where the structure is "locked" in place, i.e. where the displacements are fixed at 0. $1$s indicate the presence, and $0$s the absence of homogeneous Dirichlet boundary conditions. Currently, we do not support non-homogeneous Dirichlet boundary conditions (i.e. voxels that have displacements fixed at some value $\neq 0$) since we believe that they are not required for most TO tasks.
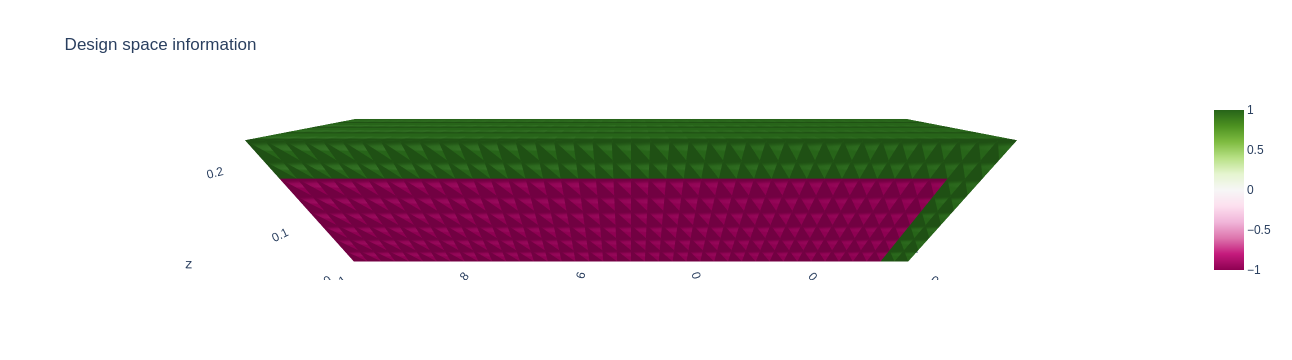
A ($1\times n_x \times n_y \times n_z$)-tensor called $\Omega_\text{design}$ containing values $\in \left\lbrace 0,1,-1\right\rbrace$ that we use to encode design space information. We use $0$s and $1$s to constrain voxel densities to be $0$ or $1$, respectively. Entries of $-1$ indicate a lack of density constraints, which signifies that the density in that voxel can be freely optimized.
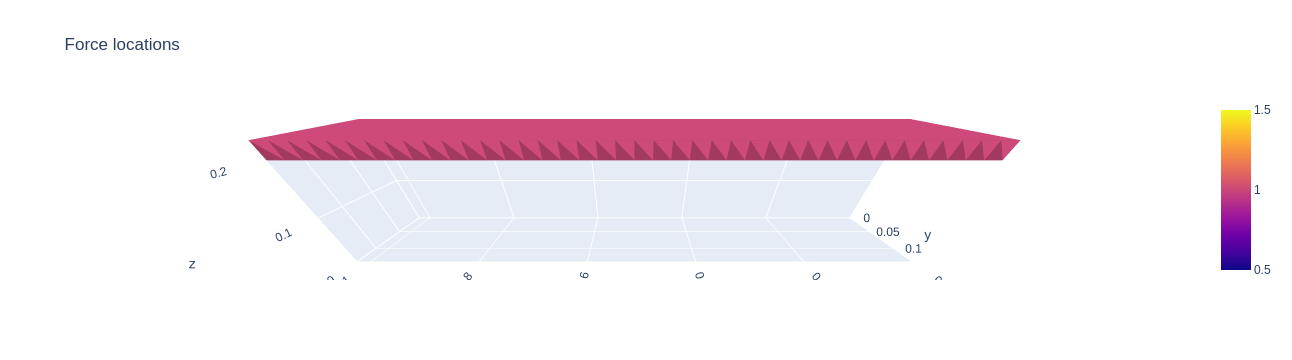
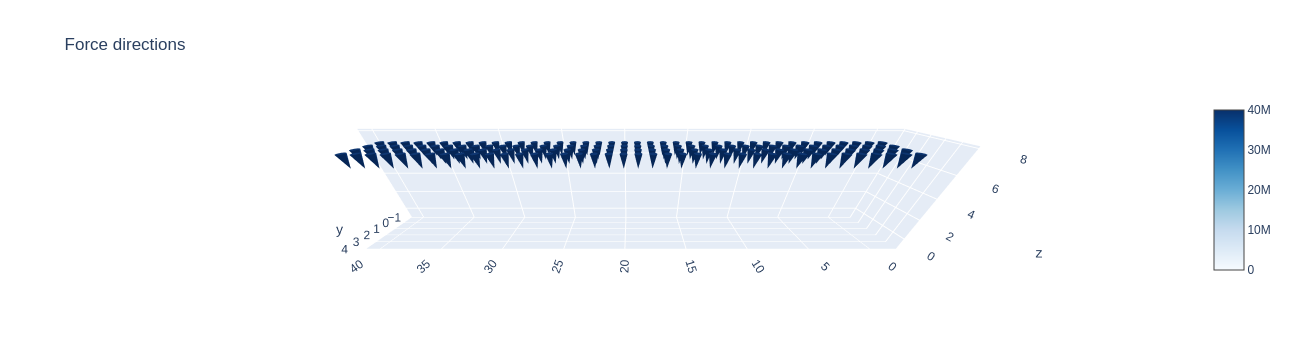
A ($3\times n_x \times n_y \times n_z$)-tensor called $F$, which encodes external forces given in $\text{N}/\text{m}^3$. The three channels correspond to the force magnitudes in each spacial dimension. For voxels that have external loads assigned to them we automatically enforce the corresponding density value to be $1$.
import torch
# scalar material properties
E = 7e10 # Young's modulus (in Pascal)
ν = .3 # Poisson's ratio
σ_ys = 4.5e8 # Yield stress (in Pascal)
shape = [40, 4, 8] # number of voxels in x, y and z direction
h = [0.0250, 0.0250, 0.0250] # spacial dimensions of each voxel in x, y and direction (in meters)
# define external forces
F = torch.zeros(3, *shape)
F[-1, :, :, -1] = -4e7 # external forces (in Newton)
# define locations of homogeneous Dirichlet conditions
Ω_dirichlet = torch.zeros(3, *shape)
Ω_dirichlet[:, 0, :, :] = 1
# define design space
Ω_design = -torch.ones(1, *shape) # -1s indicate that these voxels can be freely optimized
Ω_design[:,:2,:,:] = 1. # we set densities to 1 where there are Dirichlet boundary conditions
Ω_design[:,:,:,-2:] = 1. # we set densities to 1 where there are external forces
problem = Problem(E, ν, σ_ys, h, Ω_dirichlet, Ω_design, F)
camera_position = (0, 0.35, 0.2)
problem.plot(camera_position=camera_position,
show_axislabels=True,
show_ticklabels=True,
display=False)